|
Ampere's LawStaff posted on November 10, 2006 |
Ampere's Law
|
Definition of the ampere:
If two long, parallel wires 1 m apart carry the same current and the force per unit length on each wire is 2x10-7 N/m, then the current is defined to be 1 A.
Consider two long, straight, parallel wires separated by a distance a and carrying currents I1 and I2 in the same direction. We can easily determine the force on one wire due to a magnetic field set up by the other wire. Wire 2, which carries a current I2, creates a magnetic field B2 at the position of wire 1. The direction of B2 is perpendicular to wire1.
|
|
|
|
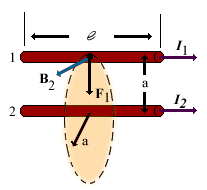
The magnitude force on a length l of wire 1 is
|
|
|
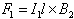
Sincel is perpendicular to B2, the magnitude of F1 is |
|
|
|
|
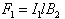
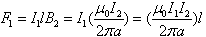
We can rewrite this in terms of the force per unit length as
|
|
|
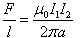
The numerical value of 2x10-7 N/m is obtained from the equation above with I1= I2= 1 A and a = 1 m.
The Ampère's law states that the line integral of B.ds around any closed path equals 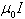 , where I is the total steady current passing through any surface bounded by closed path
|
 |
| Ampère's law is valid only for steady currents and is useful only for calculating the magnetic field of current configurations having a high degree of symmetry. |