|
RadiationStaff posted on October 23, 2006 |
Radiation
|
|
|
Thermal radiation is energy emitted by matter that is at a finite temperature. Although we focus primarily on radiation from solid surfaces, emission may also occur from liquids and gases. Regardless of the form of matter, the emission may be attributed to changes in the electron configurations of the constituent atoms or molecules. The energy of the radiation field is transported by electromagnetic waves (or alternatively, photons). While the transfer of energy by conduction or convection requires the presence of a material medium, radiation does not. In fact, radiation transfer occurs most efficiently in a vacuum.
The maximum flux (W/m2) at which radiation may be emitted from a surface is given by the Stefan–Boltzmann Law
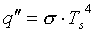
|
|
|
where Ts is the absolute temperature (K) of the surface and s is the Stefan–Boltzmann constant (s = 5.67 X 10-8 W/m2 · K4). Such a surface is called an ideal radiator or blackbody. The heat flux emitted by a real surface is less than that of the ideal radiation and is given by
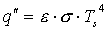
|
where e is a radiative property of the surface called the emissivity. This property, whose value is in the range 0 = å = 1, indicates how efficiently the surface emits compared to an ideal radiator. Conversely, if radiation is incident upon a surface, a portion will be absorbed, and the rate at which energy is absorbed per unit surface area may be evaluated from the knowledge of a surface radiative property termed the absorptivity á. That is,
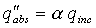
|
0 = á = 1. Whereas radiation emission reduces the thermal energy of matter, absorption increases this energy.
Assuming the surface to be one for which á = å, the net rate of radiation heat exchange between the surface and its surroundings expressed per unit area of the surface, is
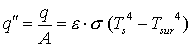
|
|
The surface within the surroundings may also simultaneously transfer heat by convection to the adjoining gas. The total rate of heat transfer from the surface is then the sum of the heat rates due to the two modes. That is,
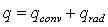
or,
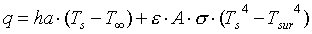
Excerpt from: Incroprera, Frank and De Witt, David P. Introduction to Heat Transfer. Second Edition. New York: John Wiley & Sons, Inc. 1985, 1990.
Copyright © 1985, 1990, by John Wiley & Sons, Inc.
This material is used by permission of John Wiley & Sons, Inc.
|