| |
If there are k positions in a sequence, and n1 distinguishable elements can occupy position 1, n2 can occupy position 2, ... and nk can occupy position k, the number of distinct sequences of k elements each is given by
|
|
N (k | n1, n2, …, nk) = n1n2…nk (B.1)
|
For example, if a design involves three parameter φ1, φ2, φ3, and there are, respectively, 2, 3, 4 values of these parameters, the number of feasible design is
|
|
N (3 | 2, 3, 4) = (2) (3) (4) = 24
|
In a set of n distinct elements, the number of k-element ordered sequences, or arrangements, is:
|
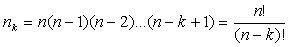 (B.2) (B.2) |
|
For example, if no digits are repeated, the number of four-digit figures is (10)4 = (10) (9) (8) (7) = 5040, whereas, if the digits can be repeated the number of four-digit figures would be (10)4 = 10,000—the latter case would include 0000 as one of the figures.
|
| |
| Combination |
| |
In a set of n distinguishable elements, the number of possible subsets of k different elements each (regardless of order) is given by the binomial coefficient
|
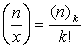 (B.3) (B.3) |
Equation B.3 is defined only for k ≤ n. Using Eq. B.2 for (n)k, we have
|
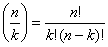 (B.3a) (B.3a) |
For example, the number of possible samples of four cards each in a deck is:
|
|
|
Excerpt from: Ang, Alfredo H-S. and Tang, Wilson H. Probability Concepts in Engineering Planning and Design. New York: John Wiley & Sons, Inc., 1975.
Copyright © 1975, by John Wiley & Sons, Inc.
This material is used by permission of John Wiley & Sons, Inc. |